
1. 검색 알고리즘이란
* 검색 : 어떤 조건을 만족하는 데이터를 찾는 행위
- 검색과 키
ex) 전공이 경제학과인 학생을 찾아라.
: 위 예시의 조건은 전공이라는 항목이다. 이렇게 조건에서 주목되는 것이 '키'이다.
* 배열검색

- 선형검색 : 무작위로 늘어놓은 데이터의 집합에서 검색 수행
- 이진검색 : 일정한 규칙의 데이터 집합에서 빠른 검색 수행
- 해시법 : 추가와 삭제가 자주 일어나는 데이터의 집합에서 빠른 검색을 수행. 체인법과 오픈주소법이 있음.
* 검색 알고리즘의 선택
- 단순히 검색만 잘되면 좋다고 생각한다면 계산시간이 짧은 검색 알고리즘을 선택할 수 있다.
- but, 검색 뿐 아니라 데이터의 추가·삭제도 수행한다면 검색이외에 작업에 들어가는 비용을 종합적으로 평가해야한다.
- 따라서 선택할 수 있는 다양한 알고리즘이 있다면 용도, 목적, 속도, 자료구조 등 여러가지 사항을 고려해야겠다.
2. 선형검색
* 선형검색
- 직선모양의 배열에서 순서대로 검색하는 알고리즘이다. 순차검색이라고도 불린다.
- 검색할 값을 찾으면 검색이 종료된다고 할 때, 이 조건을 판단하는 횟수는 평균 n/2 이다.
lst = ['s','t','u','d','y']
key = input('검색할 알파벳을 입력하시오 :')
i = 0
while True :
if i == len(lst):
idx = -1
break
if lst[i] == key :
idx = i
break
i += 1
if idx == -1 :
print('찾는 알파벳이 존재하지 않습니다.')
else :
print(f'검색하신 알파벳은 {idx+1}번째에 있습니다.')
# 검색할 알파벳을 입력하시오 :d
# 검색하신 알파벳은 4번째에 있습니다.
- 선형검색은 원소의 값이 정렬되지 않은 배열에서의 유일한 검색법이다.
* 보초법
- 앞서 나온 선형 검색은 반복할 때마다 2가지 종료 조건을 체크한다. 이 과정이 계속 반복되면 종료조건을 검사하는 비용이 커진다.
- 보초법은 배열의 끝에 도달했는가에 대한 판단을 삭제하여 위 비용을 반으로 줄인다.
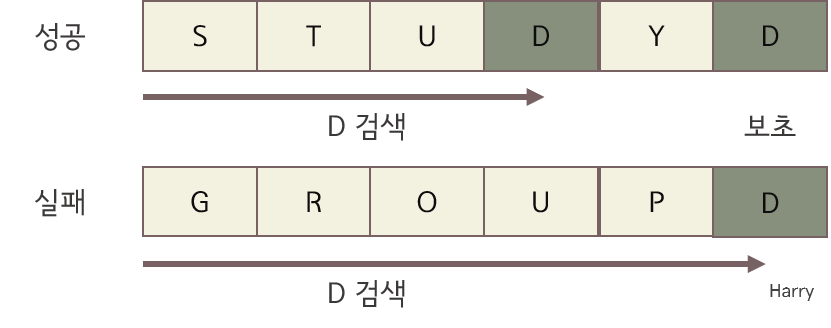
- 따라서 위에서 작성한 코드에서 보초 값을 추가하면 if i == len(lst)를 삭제하여 if문의 판단 횟수를 반으로 줄이게 된다.
- but, 반복문의 끝에 i가 길이값과 같으면 검색이 실패한것이라는 if문을 추가해야하므로 판단횟수가 1회 증가한다.
3. 이진검색
* 이진검색
- 오름차순이나 내림차순으로 정렬된 배열에서 좀 더 효율적으로 검색이 가능한 알고리즘이다.

: 가운데를 기준으로 검색범위를 절반씩 줄여나가고 있다.
- 따라서 이진검색은 중앙값이 key와 일치할 때와 검색범위가 더 이상 없는 경우에 종료된다.
* 이진검색의 실행

: 마지막의 상황에서 중앙값인 pc=7이 키인 10보다 작으므로 pl = pc+1 = 0+1 이된다. 즉 pr=0 이고 pl=1이므로 검색이 종료된다.
lst = [7, 11, 35, 55, 67, 78, 92]
key = int(input('검색할 숫자를 입력하시오 :'))
pl = 0
pr = len(lst) - 1
while True:
pc = (pl + pr) // 2
if lst[pc] == key:
idx = pc
break
elif lst[pc] < key :
pl = pc + 1
else:
pr = pc - 1
if pl > pr :
idx = -1
break
if idx == -1 :
print('검색하신 숫자가 존재하지 않습니다.')
else :
print(f'검색하신 숫자는 {idx+1}번째에 있습니다.')
# 검색할 숫자를 입력하시오 :10
# 검색하신 숫자가 존재하지 않습니다.
- 이진검색 알고리즘은 반복할 때마다 검색 범위가 거의 절반으로 줄어들므로 검색횟수는 평균 log n 이다.
* 복잡도
- 알고리즘의 성능을 평가하는 기준이다.
- 시간 복잡도 : 실행하는 데 필요한 시간을 평가
- 공간 복잡도 : 메모리와 파일 공간이 얼마나 필요한지 평가
- 가장 위에서 했던 코드 중 일부를 활용하여 다음 선형 검색 알고리즘의 시간 복잡도를 알아보자.
i = 0
while True:
if i == len(lst):
idx = -1
break
if lst[i] == key:
idx = i
break
i += 1
: 여기서 i = 0 과 같은 경우 반드시 1번만 실행됨을 알 수 있다. 그리고 while구문이나 if구문의 경우 평균실행횟수는 n/2이다.
- 1번만 실행되는 경우 복잡도 : O(1)
- 실행횟수 n/2와 같이 n에 비례하는 복잡도 : O(n)
위의 경우 계산 시간은 O(1)이 아니라 O(n)에 따름을 알 수 있다.
즉 여러 개의 계산으로 구성된 알고리즘의 복잡도는 차원이 더 높은 쪽의 복잡도를 우선으로 한다.
이를 나타내면 다음과 같다.
O( f(n) ) + O( g(n) ) = O( max( f(n), g(n) ) )
- 따라서 이진검색 알고리즘의 경우 복잡도는 O( log n ) 이다.

참고
이 글은 ‘이지스퍼블리싱’의 ‘자료구조와 함께 배우는 알고리즘 입문’을 공부 후 정리하며 쓴 글입니다.
작성된 모든 내용과 코드는 교재 및 관련 사이트를 참고하여 직접 재구성하였습니다.
Do it! 자료구조와 함께 배우는 알고리즘 입문 - 파이썬 편
http://www.easyspub.co.kr/20_Menu/BookView/381/PUB
www.easyspub.co.kr
이지스퍼블리싱 스터디룸 카페
Do it! 스터디룸 : 네이버 카페
Do it!, 된다 시리즈 책으로 함께 공부하고 서로 돕는 사람들을 만나 보세요. python, C, java, Android
cafe.naver.com
교재 공식 깃허브
easysIT/doit_dsalgo_with_python
Do it! 자료구조와 함께 배우는 알고리즘 파이썬 편. Contribute to easysIT/doit_dsalgo_with_python development by creating an account on GitHub.
github.com
'Computer Science > Algorithm' 카테고리의 다른 글
| <알고리즘> 삽입정렬과 병합정렬 (0) | 2021.12.20 |
|---|---|
| <알고리즘> 버블정렬과 선택정렬 (0) | 2021.02.03 |
| <알고리즘> 재귀 알고리즘 (1) (0) | 2020.11.29 |
| <알고리즘> 검색 알고리즘(2) (0) | 2020.11.08 |
| <알고리즘> 알고리즘 기초 (0) | 2020.10.18 |




