
1. 퀵 소트와 힙 소트
* 퀵 소트
- 퀵 소트(Quick Sort)는 병합 정렬(Merge Sort)와 마찬가지로 분할 정복 알고리즘을 활용한다. 그러나 병합 정렬과 달리 배열을 비균등하게 분할하여 정렬을 수행한다.
- 퀵 소트는 불안정 정렬에 속한다.
- 퀵 소트는 어떤 과정으로 정렬을 하는 것일까. 오름차순 정렬을 한다고 가정하자. 먼저 배열 내의 요소를 하나 선택한다. 이는 기준이 되는 원소로 피벗(pivot)이라 칭한다. 피벗을 기준으로 피벗보다 작은 원소는 피벗의 왼쪽으로 옮겨지고, 큰 원소는 피벗의 오른쪽으로 옮긴다.
- 위의 과정을 한 번 거친 후, 피벗을 제외하고 왼쪽 배열과 오른쪽 배열에 대해 각각 같은방식으로 정렬한다. 부분 배열이 더 이상 분리가 불가능할 때까지 반복한다. 그러면 정렬된 배열을 얻을 수 있다.
- 예시를 통해 더 자세히 알아보자.

- 정렬되지 않은 위와 같은 배열이 있다. 5를 피벗으로 하여 정렬이 시작된다.

- 1 부터 탐색을 시작하여 피벗 원소보다 작은 값들은 왼쪽에, 큰 값들은 오른쪽에 배치시켰다. 그 후 5를 제외하고 다시 피벗을 설정하여 같은 방식을 수행한다. 해당 방식은 코드에 따라 조금씩 차이가 있을 수 있다. 예를 들면 필자는 1부터 7까지 순서대로 비교했지만 1과 7, 6과 2 와 같은 순서로 비교할 수도 있다. 하지만 피벗을 기준으로 왼쪽과 오른쪽으로 나뉘는 것에는 변함이 없다.
- JavaScript로 간단하게 구현하면 아래와 같다.
function quickSort(arr) {
if (arr.length <= 1) return arr;
const pivot = arr[0];
const left = [];
const right = [];
for (let i = 1; i < arr.length; i++) {
const value = arr[i]
if (value <= pivot) left.push(value);
else right.push(value);
}
const sortedLeft = quickSort(left);
const sortedRight = quickSort(right);
return [...sortedLeft, pivot, ...sortedRight];
}
- arr 의 첫 원소를 피벗으로 설정하고 그 이후 원소부터 탐색하여 left와 right 를 나눈다. 그 후 각각에 대해 다시 정렬을 수행하여 합친다.
* 힙 소트
- 힙 소트(Heap Sort)는 용어에서 알 수 있듯 힙 자료구조를 사용한다. 힙은 최댓값과 최솟값을 쉽게 추출할 수 있는 자료구조이다.
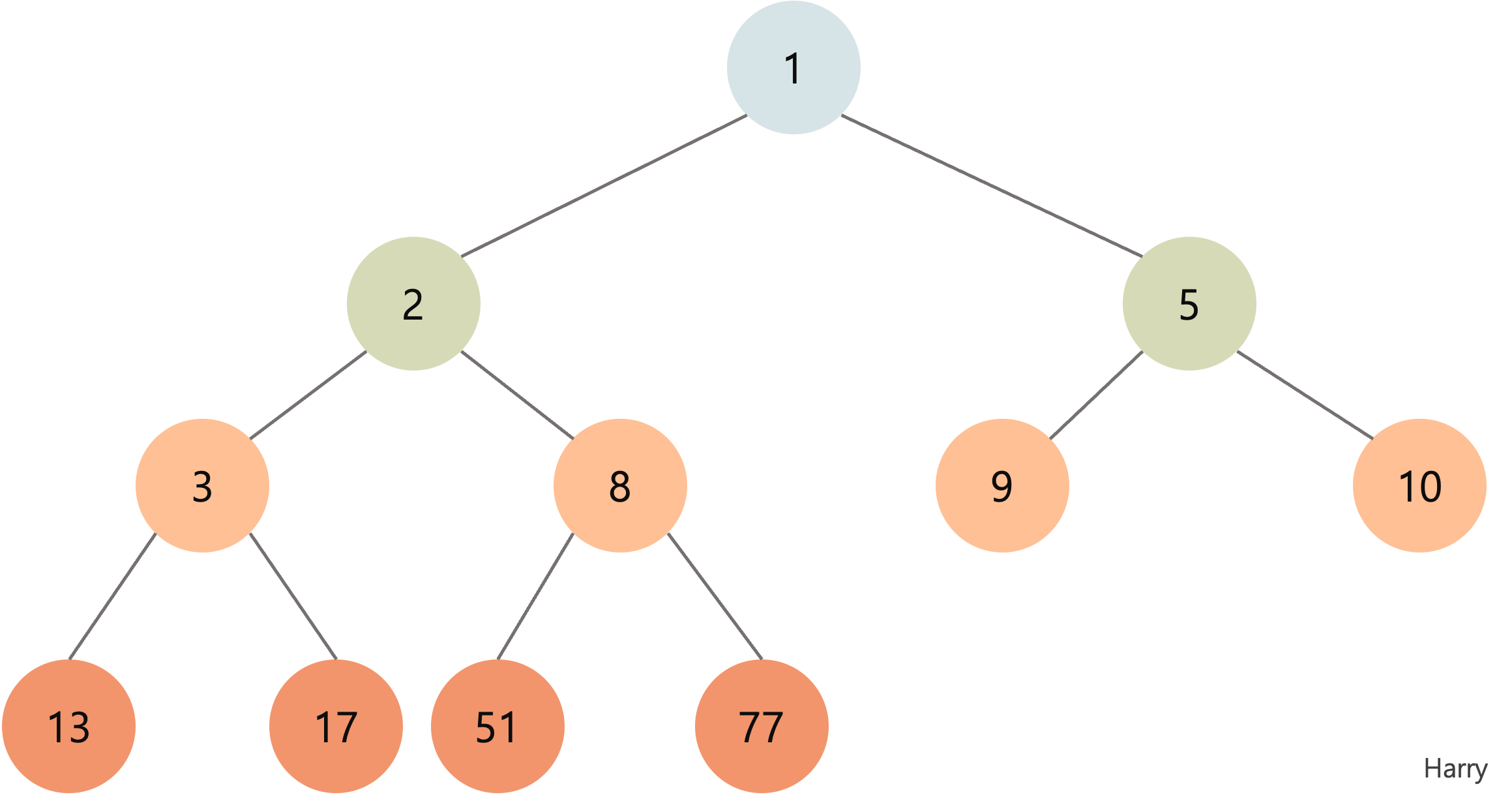
- 힙 자료구조에 대한 자세한 설명은 생략하겠다. 힙은 완전 이진트리의 일종으로 주로 우선순위 큐에서 활용한다.
- 위 이미지는 최소 힙에 대한 그림이다. 최소 힙은 자식 노드의 값보다 부모 노드의 값이 항상 작은 구조를 의미한다.
- 위와 같은 최소 힙의 경우 오름차순 정렬에서 활용할 수 있다. n 개의 원소들을 최소힙으로 만들고, 한 번에 하나씩 원소를 꺼내어 배열에 저장하면 끝이다.
2. 시간 복잡도
* 퀵 소트
- 퀵 정렬은 이상적인 경우 시간 복잡도가 Ω(N logN)이다. 왜냐하면 위에서 분할되는 상황을 봤을 때, 정확히 절반씩 나눠진다고 생각해보라. 호출의 깊이는 logN 이 될 것이다. 비교연산은 각 호출마다 n번이 일어난다. 따라서 N * logN 이 성립하게 된다.
- 그러나 퀵 소트는 최악에 상황에서 시간 복잡도가 O(N^2)이 된다. 정렬된 상황을 가정해보자. 1부터 9까지 정렬되어 있다면, 1이 피벗으로 설정되면 2~9를 다시 분할 정복할것이고, 3~9를 분할정복할 것이며 이러한 과정이 반복된다. 즉 호출의 깊이가 N이다. 물론 각 호춣마다 모든 원소를 비교해야하므로 비교연산도 N이다. 즉 N^2 이 도출된다. (참고로 퀵 소트에서 이동연산은 매우 적으므로 무시한다.)
- 위와 같은 최악의 상황에도 불구하고 퀵 소트는 Quick 이라는 이름을 쟁취하였다. 왜일까. 퀵소트는 평균 시간 복잡도가 θ(N logN) 이며 대부분의 프로그래밍에서 보장한다. 이것이 가능한 이유는 적당한 숫자로 피벗을 잘 고르기 때문이다.
- 피벗을 고르는 방식은 크게 2가지 정도로 나뉜다. 첫째, 배열의 전체 값 중 아무 숫자나 피봇으로 잡는 난수를 고르는 방법이 있다. 최악의 경우는 정렬이 되어있을 경우인데, 이 때 최악의 피봇을 선택할 확률은 1/N 이며, 매 호출마다 최악의 피봇이 선택될 확률은 그 제곱이다. 둘째, Median-of-Three Partition을 사용한다. 배열의 처음, 가운데, 끝 값을 비교하여 가운데 값을 피봇으로 선정하는 것이다. 실제로 가장 많이 사용되는 방법이며 여기에 몇 가지 다른 스킬들이 들어간다고 한다.
- 어쨌든 N logN에 가깝게 나온다는 것은 알았다. 그렇다면 N logN 복잡도를 가진 병합정렬은 왜 Quick이라는 이름을 쟁취하지 못하였을까. 그 이유는 피벗에 있다. 피벗은 한 번 결정된 순간 그 이후 연산에서 제외된다. 따라서 같은 복잡도를 가진 정렬에 비해 퀵 소트가 가장 빠르다.
* 힙 소트
- 힙 소트의 복잡도는 힙에 영향을 받는다. 힙은 하나의 원소를 삽입하거나 삭제할 때 힙을 다시 배치하는데 logN이 걸린다. 원소의 개수가 n이므로 전체적으로 삽입과 삭제마다 N logN이라는 시간이 걸린다.
- 따라서 힙 소트의 복잡도는 최선,최악, 평균 모두 N logN을 갖는다.
- 힙소트가 유용한 경우는 전체 자료를 정렬하기보다 가장 큰 값 또는 가장 작은 값 몇개만 필요할 때이다.
참고
[알고리즘] 퀵 정렬(quick sort)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
퀵 정렬 - 위키백과, 우리 모두의 백과사전
퀵 정렬(Quicksort)은 찰스 앤터니 리처드 호어가 개발한 정렬 알고리즘이다. 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다. 퀵 정렬은 n개의 데이터를 정렬할 때, 최악의 경우에
ko.wikipedia.org
퀵소트 (quick sort)
병합정렬에 이어 퀵소트(quick sort)를 다뤄보려고 합니다. 퀵소트의 평균 시간복잡도는 O(NlgN)입니다....
blog.naver.com
힙 정렬 - 위키백과, 우리 모두의 백과사전
힙 정렬(Heap sort)이란 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법으로서, 내림차순 정렬을 위해서는 최대 힙을 구성하고 오름차순 정렬을 위해서는 최소 힙을 구성하면 된다. 힙 정
ko.wikipedia.org
[알고리즘] 힙 정렬(heap sort)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
'Computer Science > Algorithm' 카테고리의 다른 글
| <알고리즘> 퀵정렬은 병합정렬보다 항상 좋은 선택인가 (0) | 2022.10.30 |
|---|---|
| <알고리즘> 삽입정렬과 병합정렬 (0) | 2021.12.20 |
| <알고리즘> 버블정렬과 선택정렬 (0) | 2021.02.03 |
| <알고리즘> 재귀 알고리즘 (1) (0) | 2020.11.29 |
| <알고리즘> 검색 알고리즘(2) (0) | 2020.11.08 |





